最优化方法复习笔记（六）共轭梯度法

当前位置：主页 > 新闻资讯 > 公司新闻

最优化方法复习笔记（六）共轭梯度法！

发布于 2024-07-01 13:58 阅读（）

上一章传送门：

https://zhuanlan.zhihu.com/p/338829644

没想到呀，写CG的手感这么好。一天就写了1w字，美汁汁。

好啦好啦，copy完本地的markdown就去写欠课题组的模型啦（摸了）

事实是，数据结构课设没写完+毛概没复习的我可能会和舍友来一场CS欢乐赛。不会有人觉得CS是computer science的简称吧。不会吧，不会吧。（当然，希望导师这么认为>_<）

2021.8.16

笔者老咸鱼现在开始完善这些笔记，我会开始慢慢加入一些动画，manim源码在我的GitHub仓库中：

https://github.com/LSTM-Kirigaya/OptimizeNote

有兴趣的同学以及manim的同好可以一起看看。

目录（传统艺能）

回顾梯度下降法
共轭方向

hook
从正交到共轭
二次型的共轭方向怎么找
共轭方向法的框架

共轭梯度法

子空间扩展定理
共轭by梯度——共轭梯度法
共轭梯度法的几个性质

共轭梯度法的收敛性

共轭梯度法的收敛速率
泛化到非二次型是否可行？FR-CG共轭梯度法
FR-CG下降条件
重开始策略

总结

还记得梯度下降法吗？这个方法算是我们最优化之路上的hello world了。它的迭代式为：

$x_{k+1}=x_k-\\alpha_k \ abla f(x_k)\\\\$

由于算法比较简单，其收敛性分析也有比较nice的结果。我们当初为了一个漂亮的结果，我们将梯度下降法研究的目标限制到了满足强凸和光滑的函数，即我们研究函数的Hessian矩阵 $\ abla^2f(x)$ 的谱范数限制到 $\\mu$ 和 $\\mathcal L$ 之间，其中的 $\\mu$ 和 $\\mathcal L$ 分别是我们假设的强凸系数和光滑系数，如果我们研究的函数满足上述性质，那么在对它实施梯度下降时，我们能保证算法的收敛速率是线性的：

$\\frac{|f(x_{k+1})-f(x^*)|}{|f(x_k)-f(x^*)|}\\le 1-\\frac{\\mu}{\\mathcal L}\\\\$

如果我们研究的函数是二次型的话，那么根据我们之前的一堆推导，我们可以舒服地把收敛速率的界拉得更紧：

$\\frac{|f(x_{k+1})-f(x^*)|}{|f(x_k)-f(x^*)|}\\le(1-\\frac{2}{1+\\kappa})^2\\\\$

其中的 $\\kappa$ 是二次型的条件数，也就是最大特征值与最小特征值的比值。

但是梯度下降法只在小领域内是最快的，因此算法鲁棒性较差，对于一般的二次型，若条件数较大，抖动下降将成为梯度下降法的常态，所以梯度下降法的下降速度不是很快，而且还会来回跳动，所以梯度下降法也很不稳定。

在实际的任务中，我们很少会直接使用梯度下降法优化目标，比如在手写数字识别的任务上，如果我们使用梯度下降法来优化损失函数，那么训练结果如图所示。

可以看到，训练集上的损失值无法下降，正在训练模型的你直接气到原地爆炸。

如果我们换一个优化器，比如，我们使用Adam优化器，那么得到的训练结果如下图。

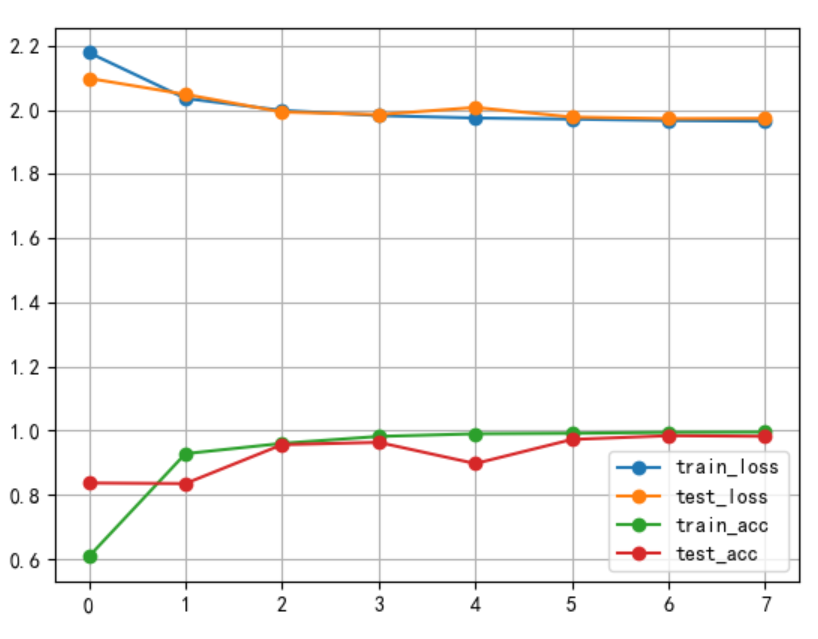
可以看到，训练结果堪称完美，无论是训练集还是测试集，最终的准确率都接近百分之百。

所以在神经网络的结构完全相同，各项超参数一致的情况下，优化算法对结果的影响有多大，不言而喻。而我们上面使用的优化器Adam的一部分是借鉴了动量法，而动量法的理论最优情况就是这次要讲的共轭梯度法了。

上述训练过程的代码可以在我之前的一篇拙笔中找到：

https://zhuanlan.zhihu.com/p/293888589

为了（尽可能）做一个共轭梯度法的好的storyteller，在正式讲梯度下降法之前，有必要讲讲此处的共轭方向。

如果你急于实现CG，不妨直接跳到后面的共轭梯度法。因为之前的笔体for认知。

先来个引子。假设我们现在要优化的函数为：

$f(x)=x_1^2+x_2^2\\\\$

如果使用梯度下降法，我们会求取它的梯度，然后根据梯度和步长来更新我们的迭代点，请注意，我们这里的更新迭代点是一次性将这个迭代点的各个维度的量都更新了。但是其实? $x_1$ 和 $x_2$ ?是两个不相干的变量（我们一般称之为解耦合的）， $x_1$ ?的变化关? $x_2$ 什么事？所以我们完全可以把上述的优化问题看成两个单独的单变量优化问题。而对于单变量优化问题，其搜索方向是固定的，要确定的只有步长而已，这么做会简单很多。

比如这个问题，由于 $x_1$ ?和 $x_2$ ?是解耦合的，所以我们可以分别以 $x_1$ ?和 $x_2$ ?为自变量优化这个函数，比如先优化 $x_1$ ?，再优化 $x_2$ ?。优化 $x_1$ ?，也就是等价于以 $d_1=(1,0)^T$ ?为搜索方向，因为 $x_2$ 在这个方向的分量为0，所以以这个方向为搜索方向进行更新是不会影响 $x_2$ ?的值的；同理，如果我们想要只更新? $x_2$ ，那么只要以? $d_2=(0,1)^T$ 为搜索方向就可以了。你会发现，我们选取的两个搜索方向是正交的，这其实就是特殊情况下的共轭方向法。

而这样更新的趋势也很明显，我们可以在二维平面中可视化出来，我们选取 $(1,1)^T$ ?为迭代初值，那么梯度下降法和共轭方向法的更新轨迹如下图所示：

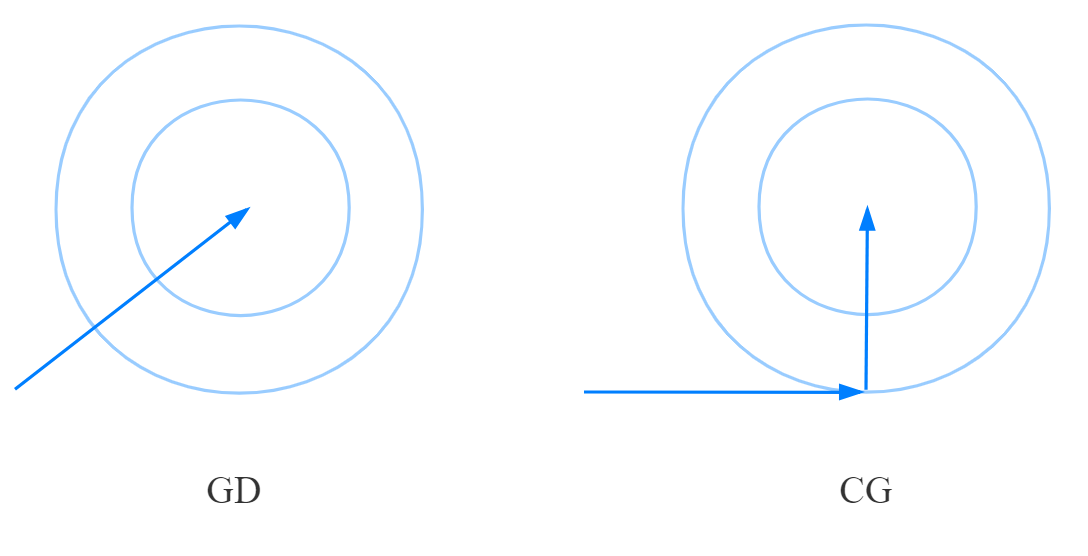
上述的两个过程的动画演示如下（manim制作）：

使用GD优化二次型https://www.zhihu.com/video/1410701495906443264

使用CG优化二次型https://www.zhihu.com/video/1410701831006195712

你或许会说，共轭方向法需要的步骤怎么反而更多了，按两个方向来走貌似显得鸡肋了。别忘了，梯度下降法的收敛速率：

$\\frac{|f(x_{k+1})-f(x^*)|}{|f(x_k)-f(x^*)|}\\le(1-\\frac{2}{1+\\kappa})^2\\\\$

而我们刚刚优化的函数可以写成

$f(x)=\\frac12x^TQx\\\\$

其中的 $Q=\\begin{pmatrix}2&0\\\\0&2 \\end{pmatrix}$ ?，它的条件数为1，所以必然一次迭代就达到最优点。那么如果我们选取梯度下降法的软肋，也就是大条件数的二次型，那么两者又会如何呢？我们不妨把Hessian矩阵拉伸成 $Q=\\begin{pmatrix}4&0\\\\0&2\\end{pmatrix}$ ?，再试试刚才的过程，并看看GD和共轭方向法的收敛轨迹：

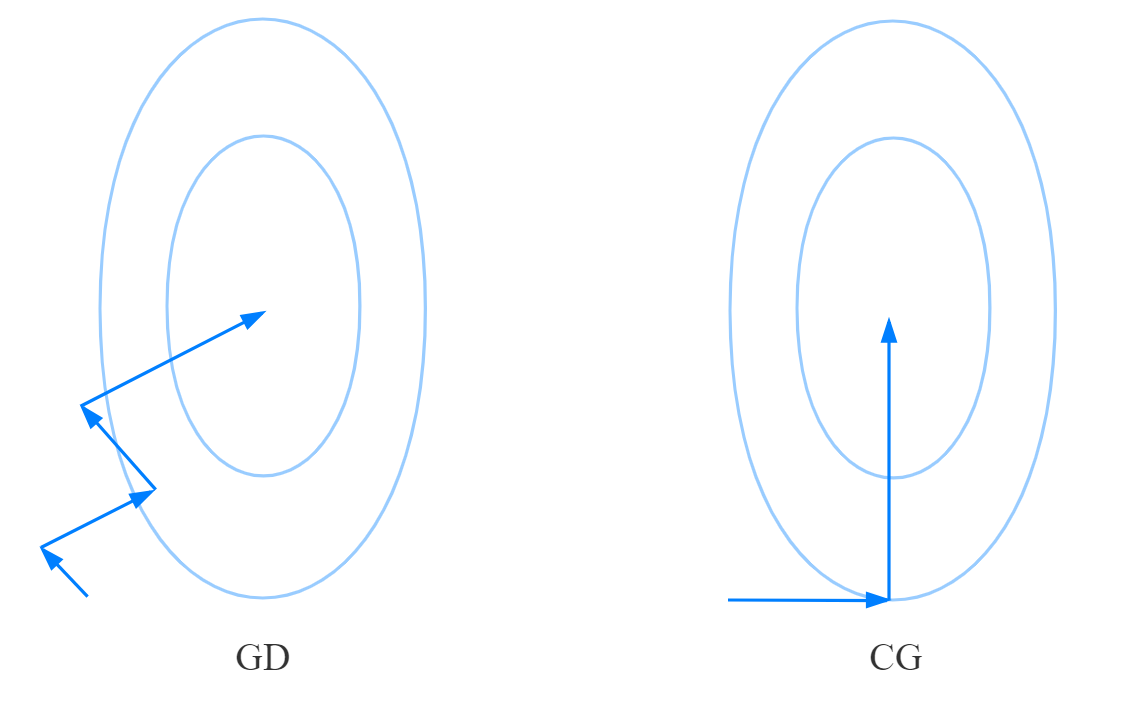
可以看到GD需要经过四次迭代，而共轭方向法只需要经过两次迭代就可以了。而且随着条件数的增大，GD的迭代次数会越来越多，但是共轭方向法却只要两次迭代。

其实这也很好解释：GD每次更新一般都会改变迭代点的所有维度的值，因此，每次迭代一次后得到的迭代点就不一定是之前搜索方向上的最优点了。反观共轭方向法，共轭方向法每次只在影响一个维度的方向上搜索，就以上图为例，在更新完 $x_1$ ?后，共轭方向法选择朝 $d_2$ ?这个方向搜索，而 $d_2$ ?和? $d_1$ 是正交的，因此第二次搜索不会改变迭代点的第一个维度，也就是不会对第一次搜索得到的成果造成影响。而GD算法的每一次搜索都会对上一次搜索的成果造成影响。

相信你已经有点感性的认识了，如果我们要优化的目标类似于上面那个椭圆（椭圆的各个轴与坐标轴平行），那么我们的共轭梯度法就会表现为逐维度搜索（也就是沿着坐标轴搜索），每次搜索只更新迭代点一个维度的值，而且每次迭代保证那个维度达到最优，那么如果优化目标的空间是 $n$ ?维空间，那么我们至多经过? $n$ 次搜索就可以达到最优点，而且这个次数与Hessian矩阵的条件数无关。

从上述的例子我们可以看到，使用共轭梯度法解决标准的二次型时，我们为了保证逐维度搜索，也就是每次只更新一个维度，也就是让每次更新的维度不影响别的维度，我们需要保证我们选取的搜索方向相互正交。然而相互正交的搜索方向并不是共轭梯度法得到方向。共轭梯度法嘛，得到的搜索方向肯定时相互共轭的呀。

刚刚接触到这个概念，你估计是一脸懵逼：共轭是啥？共轭长什么样？为什么到处都听到共轭，但是具体抽象到向量之间的共轭，又无法描述？莫急，我还是通过画图的方式，先给你一个关于共轭感性的认识。

我们刚才所要优化的目标函数是一个二次型，而且这个二次型的等高线的椭圆是一个标准的椭圆，它的两个轴分别与坐标轴平行。那如果我们要优化的二次型的椭圆是稍微“斜一些”的呢？

如果我们还是保持正交的姿态来选取搜索方向显然是不行的。第二个方向应该如右图所示向右偏一点，就好像我们第二个搜索方向随着这个椭圆的偏移也发生了相应的偏移。事实上，我们完全可以从另一个角度来看待这个问题，那么你就会发现，这个方向的得到很明显，回到我们原本的标准椭圆的优化情况，我们现在研究的这个偏移的椭圆实际上可以对原本的标准椭圆所在的空间做一个线性变换得到，我的意思是下面这张图：

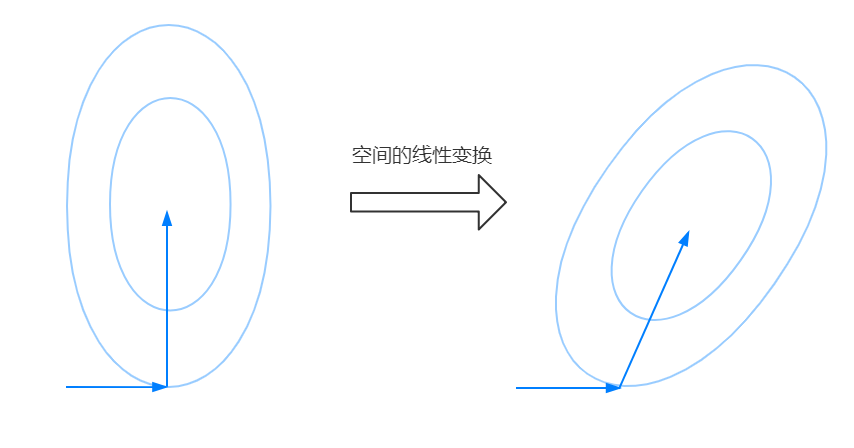
通过线性变换后，原本正交的两个方向不正交了，但是它们和椭圆贴合得还是很好，你或许感觉到了，用正交来描述这种不同的线性空间内得方向组得关系貌似并不完备，总感觉这两个搜索方向之间的关系可以用一个不变的量来描述，这个量不会随着线性空间选取的不同而发生什么变化。

没错！You are near the gate！这种关系其实就是我想说的共轭，在共轭梯度法中，我们想得到的并不是一组相互正交的搜索方向，而是一组相互共轭的搜索方向。

Fine.相信你已经对共轭有了一个感性的认识。那么我们应该如何用数学语言来刻画这种关系呢？首先很明显，在标准的欧式空间中，正交与共轭等价，假设我们的两个搜索方向是 $d_1$ ?和 $d_2$ ?，那么很显然? $d_1^Td_2=0$ 。然后我们将上图中对空间的线性变换记为 $Q$ ?，那么在对空间做线性变换后，度量空间由 $I$ ?变为了 $Q$ ?，而我们搜索方向的“这种性质”依旧存在，而我们的这个变换并不是仿射变换，因此，原空间内的0在? $Q$ 度量的意义下还是0。所以? $d_1^Td_2=0$ 在线性变换后变为：

$d_1^TQd_2=0\\\\$

恭喜！你得到了共轭的表达式，虽然我们的推导看起来相当随意，就好像喝完下午茶后的聊资般廉价地难以使人信服，但是我希望你能够得到对共轭感性的认识。（没有数学系的会看我这个半吊子AI算法rookie的文章吧，应该没有吧？那我就继续胡说八道了~~）

还是给出一个看起来像那么回事儿的共轭的定义吧：

设 $Q$ ?是正定矩阵，若对于两个不同的非零向量? $d_i,d_j$ 满足：

$d_i^TQd_j=0\\\\$

则称 $d_i$ ?与? $d_j$ 是共轭方向。

接下来再说说什么收共轭向量组：如果一组方向? $d_0,d_1,...,d_{n-1}$ 中任意两个向量? $d_i,d_j$ 均满足

$d_i^TQd_j=0\\\\$

关于上述的定义，还有两个小结论：

共轭向量组中的向量一定线性无关。
若? $Q$ 是正定矩阵，则存在唯一的对称矩阵 $A$ ?使? $Q=AA$ 。我们也称矩阵? $A$ 是矩阵? $Q$ 的平方根。

结论一依靠线性无关的定义使用反证法即可证明，结论二则可以通过对称矩阵的特征值分解完成

根据刚才感性认知，你应该可以猜到这么一个事实：对于一般的二次型函数，假设最优点为? $x^*\\in\\mathbb R^n$ ，那么顺着共轭向量组走，每步的更新满足：

$\\begin{align}x_{k+1}&=x_k+\\alpha_k d_k\\\\ \\alpha_k&=\\arg\\min_{\\alpha\\in\\mathbb R}f(x_k+\\alpha d_k) \\end{align}\\\\$

那么最多走? $n$ 步就可以达到最优点了，而且还神奇地不受该死的条件数的影响。既然这么爽，那么对于一个二次型，我们怎么获得它对应的一个共轭向量组呢？

我们肯定是先从简单的说起呀，假设我们研究的二次型是 $f(x)=\\frac12x^TQx$ ?，那么当? $Q=diag(\\lambda_1,...,\\lambda_n)$ 时，这个时候，画出来的二次型等高线椭圆的各个轴与坐标轴平行。

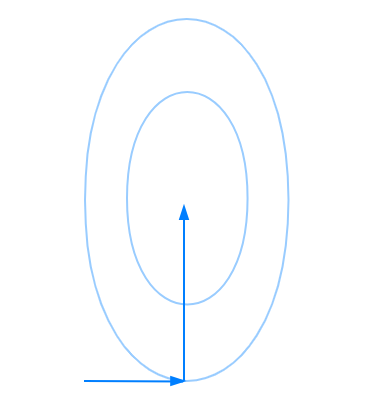
这个时候，很明显，基底向量组就是我们要的共轭向量组。不信，我们做个简单的计算，记基底向量组为? $(e_1,e_2,...,e_n)^T$ ，那么对于? $i\ ot=j$

$\\begin{align}e_i^TQe_j&=e_i^T\\begin{pmatrix}\\lambda_1\\\\ &\\lambda_2\\\\ &&...\\\\ &&&\\lambda_n \\end{pmatrix}e_j \\\\ &=e_i^T\\begin{pmatrix}0\\\\ ...\\\\ \\lambda_j\\\\ ...\\\\ 0 \\end{pmatrix}\\\\ &=0 \\end{align}\\\\$

这满足共轭的定义，因此基底向量组也就是我们要的共轭向量组。

特殊情况总是美好的，那要是我们的二次型的? $Q$ 不是对角矩阵呢？也就是那个斜着的椭圆，显然这种情况，我们的基底不是共轭的了，那么怎么办？你当然可以构造待定参数，一通暴算。但是我喜欢用已知的来诱导出未知的，我们已知什么？我们已知Hessian矩阵为对角矩阵的二次型的共轭向量组，那么我们把这种情况给它映射回去Hessian矩阵为对角矩阵的情况不就好了？这或许不能立竿见影得到我们想要的答案，但是至少是一个很nice的想法（嗯，至少我是这么认为的）

那我们试试吧！我们的目标函数是 $f(x)=\\frac12x^TQx$ ?，我们对? $x$ 做线性变换?，使得 $x$ ?变为 $Ux$ ?，那么函数就为? $\\bar f(x)=f(Ux)=\\frac12x^TU^TQUx$ 。做到这儿了，我们当然希望确定? $U$ 使得? $U^TQU$ 是对角矩阵，但是这个地方我们可以偷个懒，直接暴力 $U^TQU$ 将?变成? $I$ ：要是我们能将 $Q$ ?拆成两半，给两边的? $U$ 一人一半，然后我们把 $U$ ?取为那个一半的逆矩阵，不就可以暴力化成单位阵了吗？

由于二次型的 $Q$ ?是正定对称的（正定是大前提），因此? $Q$ 存在平方根 $A$ ?，满足 $Q=AA$ ?，所以? $f(x)=\\frac12x^TU^TAA Ux=\\frac12x^T(AU)^T(AU)x$ 。我们只要令 $U=A^{-1}$ ?不就如愿以偿了吗？由于 $A=P^{-1}diag(\\sqrt{\\lambda_1},...,\\sqrt{\\lambda_n})P$ ?，其中 $P$ ?是正交矩阵，? $\\lambda_i$ 是 $Q$ ?的第 $i$ ?个特征值。因此? $A$ 一定存在逆矩阵，所以我们的? $U=Pdiag(\\frac1{\\sqrt{\\lambda_1}},...,\\frac1{\\sqrt{\\lambda_n}})P^{-1}=P^{-1}diag(\\frac1{\\sqrt{\\lambda_1}},...,\\frac1{\\sqrt{\\lambda_n}})P$ 。

我们已经知道? $(e_1,...,e_n)$ 是Hessian矩阵为对角阵时的一组共轭向量组，我们把它们拼成一个矩阵，很显然，这个矩阵就是一个单位阵? $I$ 。那么我们在 $I$ ?的基础上将上述线性空间内的共轭向量组再映射到标准的 $I$ ?度量的空间可以得到，这组共轭向量组拼成的矩阵为? $UI=U=P^{-1}diag(\\frac1{\\sqrt{\\lambda_1}},...,\\frac1{\\sqrt{\\lambda_n}})P$ 。

所以我们想要的共轭向量组为? $(u_1,...u_n)$ ，也就是 $U$ ?的列向量组或是行向量组。

美汁儿汁儿，我们得到了我们需要的共轭向量组，它就是目标二次型的Hessian矩阵的平方根逆矩阵的列向量组。

对于正定二次型来说，我们刚才直接一下子得到了它的一组共轭向量组。然而对于一个一般的函数，想要一下获取它的一组共轭向量组很难做到，如果我们故技重施，只使用一次线性变换就妄想得到一个Hessian矩阵为对角阵的二次型未免过于理想，多次线性变换又会变得难以分析，所以，我们一般会通过迭代的方式来获取下一个与当前搜索方向共轭的方向，而不是一次获取整个共轭向量组。

因此，这确定了我们的共轭方向法算法的框架。

$\\begin{align}给定迭代初值&x_0和阈值\\epsilon>0,令k=0\\\\ 计算g_0=\ abla &f(x_0)和初始下降方向，满足d_0^Tg_0<0，重复如下步骤:\\\\ 1.\\quad&如果||g_k||<\\epsilon,停止迭代。\\\\ 2.\\quad&线搜索确定步长：\\alpha_k=\\arg\\min_{\\alpha}f(x_k+\\alpha d_k)\\\\ 3.\\quad&更新迭代点：x_{k+1}=x_k+\\alpha_kd_k\\\\ 4.\\quad&采用某种共轭方法计算得到d_{k+1},使得d_{k+1}^TGd_j=0,j=0,1,...,k\\\\ 5.\\quad&令k=k+1 \\end{align}\\\\$

注意，这是共轭方向法，共轭梯度法（CG）是实现共轭方向法的一个方法。由于CG是通过梯度信息来获取共轭方向的，所以我们称之为共轭梯度法。

如果你已经对共轭方向法有了一个大致的认识，那么接下来的共轭梯度法对你来说也不会是难事。

有了之前的铺垫，我认为下面的共轭梯度法会更好讲一些。

我们之前 $I$ 从?度量空间的映射来说明了怎么得到一组共轭向量组，但其实，我认为一些关于共轭向量组的性质也需要引出。这对于之后的推导或者对共轭梯度法的认识大有裨益。现在还是把我们研究的函数限制为正定二次型吧。在下图这种情况下时，我们的两个搜索方向是相互正交的。

不难想象，拓展到高维空间时，我们得到的若干个搜索方向也是相互正交的，也就是说我们第 $k$ ?次迭代时的方向与之前的 $k-1$ ?次迭代得到的所有搜索方向都正交，也就是说我们第? $k$ 次得到的搜索方向正交于前面? $k-1$ 次搜索方向张成的线性空间。（如果一个非零向量与一个线性空间内的所有向量都正交，那么我们称该向量正交于该线性空间）

或许你看了一遍没有看懂，又或是你看了几遍看懂了，那么我接下来的解释就显得毫无意义了hhh。请允许我尝试解释一下加粗的那句话。

之前说过共轭向量组彼此是线性无关的，线性无关的? $n$ 个向量是可以张成一个 $n$ ?维线性空间。比如我们之前的例子，我们的共轭方向是? $d_1=(1,0)^T$ 和 $d_2=(0,1)^T$ ?，它们可以张成二维线性空间，因为对于该空间中任何一个向量 $v=(a,b)^T$ ?，它都可以通过? $d_1$ 和 $d_2$ ?的线性组合得到。也就是说，如果线性无关的 $n$ ?个向量是可以张成一个? $n$ 维线性空间，那么这? $n$ 个向量可以当作这个? $n$ 维空间的基底向量组。如果你承认我们第? $k$ 次迭代时的方向与之前的 $k-1$ ?次迭代得到的所有搜索方向都正交，那么结合张成(span)的一个较为感性的认识，相信，你就可以理解我上面加粗的那句话了。

这边会有一个动态的变化，如果你想说套娃的话。我们把第 $k$ ?次得到的搜索方向记作 $d_k$ ?。

既然? $d_k$ 正交于 $d_1,...,d_{k-1}$ ?张成的线性空间，那么下一次迭代时， $d_{k+1}$ ?与 $d_1,...,d_{k-1},d_{k}$ 张成的?线性空间岂不是也是正交的？嗯哼？我想说的是，你发现了吗，我们之前的 $d_k$ ?“融入”了? $d_1,...,d_{k-1}$ 张成的线性空间中，由于这? $k$ 个向量线性无关，所以 $d_k$ ?的加入会使得张成的线性空间多了一个维度，也就说原本的子空间被拓展了维度。

Fine，如果上述的描述你能明白，那么你离子空间拓展定理不远了。只不过，我刚刚一直在讲的是 $I$ ?度量空间内的，如果我们选取的度量矩阵不是对角矩阵呢？那种情况下，即便? $k=2$ 都不满足正交的条件。

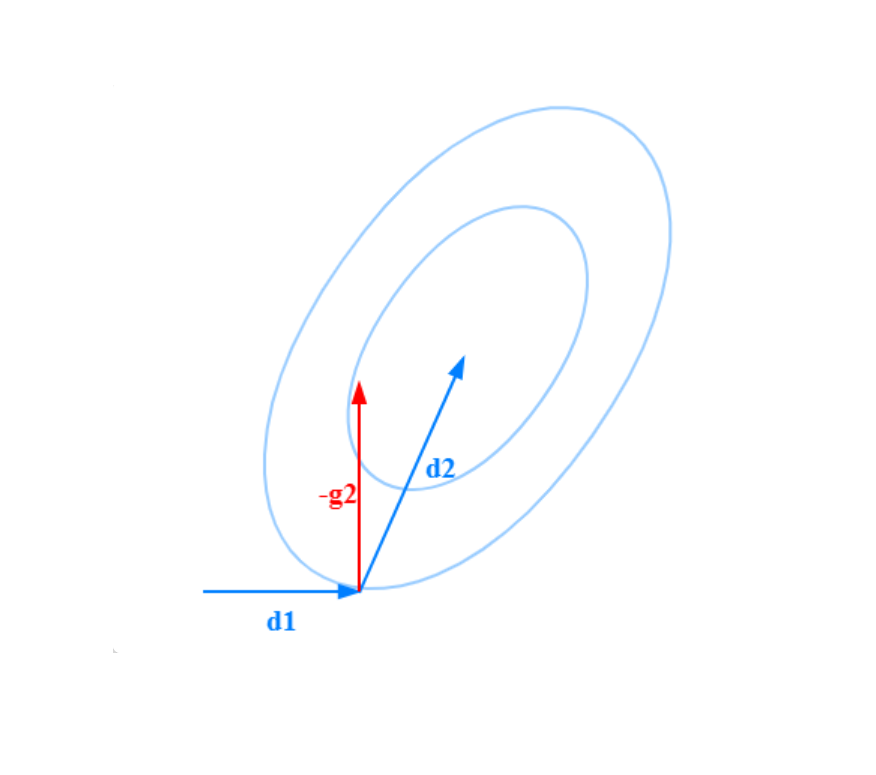
这张图就是? $k=2$ 时的情况，子空间只由?一个向量 $d_1$ 张成，而? $d_1$ 张成的是与 $d_1$ ?共线的直线，而我们后续得到的 $d_2$ ?很明显并不和这条?张成的直线正交。事实上，你会发现，虽然 $d_2$ ?不与? $d_1$ 正交，但是? $-g_2$ （也就是迭代点? $x_2$ 处的梯度反方向）与? $d_1$ 正交。当然这只是一个观察，但事实上you are near the gate。我们不妨来看看真正的子空间拓展定理：

$\\begin{align}&设G是正定矩阵,d_0,d_1,...,d_{n-1}是关于G的共轭方向组，对于二次型f(x)=\\frac12x^TGx+b^Tx\\\\ &任选迭代初值x_0,依次以各个共轭方向为搜索方向，采用精确先搜索进行迭代，则第k+1步得到的迭\\\\ &代点处的梯度方向与之前所有的搜索方向张成的线性空间正交，也就是g_k^Td_j=0,j=0,...,k-1\\\\\\\\ &其中g_k=Gx_k+b是目标函数的梯度，并且x_k是f(x)在集合X_t=\\{x\\in\\mathbb R^n|x=x_0+\\sum_{j=0}^{k-1}\\beta_jd_j,\\beta_j\\in\\mathbb R\\}\\\\ &上的极小值点。特别的，x_n是f(x)在\\mathbb R^n上的极小值点。 \\end{align}\\\\$

可以看出? $X_t$ 是? $d_0,...,d_{k-1}$ 张成的线性空间。因此，从上述定义可以看出共轭方向法的搜索逻辑：先在 $\\mathbb R$ ?上找到最棒的解，然后得到下一个共轭方向，拓展我们的搜索维度，在 $\\mathbb R^2$ ?上搜索，找到最棒的解，这样迭代下去，直到我们的搜索维度达到原问题的维度 $\\mathbb R^n$ ?，或者说我们搜索的子空间拓展到了原问题的线性空间，那么由于每次子空间上的解都是最nice的，那么我们最终拓展到的 $\\mathbb R^n$ ?上的解就原问题的最nice的解。也就是说，我们每次都是在保证我们已经在目前的这个子空间（或者说线性流形）上已经达到最优了，然后我们再拓展这个子空间的维度，直到这个子空间拓展得和我们原问题得搜索空间一样时，那么得到的解就是最好的。

你或许会担心，我们将搜索的子空间拓展一个维度再搜素后得到的解会不会破坏我们之前在那个子空间中得到的解。不要忘了我们的搜索的方向是相互共轭的。这个神奇的性质能够保证我们各个搜索方向互不影响，因此，当我们将搜索空间拓展到? $\\mathbb R^n$ 时，就能够保证得到的结果是原问题的搜索空间中最好的。

而子空间搜索定理也说明了，我们第? $k+1$ 次得到的迭代点处的梯度值与之前所有的搜索方向正交，也就是说之前所有的搜索方向再梯度方向上分量都为0，这个方向是“前人”没有探索过的方向，我们需要在这个新的方向上探索更新迭代点。这个问题是与我们之前那个? $I$ 度量的搜索是同构的。

当然上面的只是我们的感性认识，作为一名求真求实的工科生，我们还是需要认真地证明一下子空间拓展定理的。

证明：我们只需要证明对所有的? $i\\le n-1$ 都有：

$g_{i+1}^Td_j=0,\\quad j=0,...,i\\\\$

① $j=i$ ?时，根据精确线搜，有? $\\frac{\\partial}{\\partial \\alpha}f(x_i+\\alpha d_i)=\ abla f(x_{i+1})^T d_i=g_{i+1}^Td_i=0$ .

②? $j<i$ 时，我们需要充分利用? $g_{i+1}^Td_i=0$ 和共轭这个条件，所以很自然的，想办法把 $g_{i+1}^Td_i=0$ ?拆成满足前面两个条件的样子：

$\\begin{align}g_{i+1}^Td_j&=g_{i+1}^Td_j+\\sum_{k=j+1}^i(g_{k}^Td_j-g_{k}^Td_j)\\\\ &=g_{j+1}^Td_j+\\sum_{k=j+1}^i(g_{k+1}-g_k)^Td_j\\\\ &=\\sum_{k=j+1}^i(g_{k+1}-g_k)^Td_j\\quad\\quad(因为精准线搜所以g_{j+1}^Td_j=0)\\\\ &=\\sum_{k=j+1}^i[G(x_{k+1}-x_k)]^Td_j\\\\ &=\\sum_{k=j+1}^i\\alpha_kd_kGd_j=0\\quad\\quad(搜索方向相互共轭)\\\\ \\end{align}\\\\$

较为简单，我们证明了子空间拓展定理。

好吧，之前的都是一些基本的认识。我们有了关于共轭向量组的一点基本认知后，还是不知道到底如何构造或者获得一个函数在某一次搜索方向后的共轭搜索方向。事实上，由于梯度信息在优化问题是非常常用的信息，那我们不妨试试使用梯度信息来获得共轭的搜索方向。而这种通过梯度信息来实现共轭方向法的算法被我们称为共轭梯度法(conjugate gradient method)。这也是本文的重点。

共轭梯度法是一种典型的共轭方向法，搜索方向的构造要求如下：

所以的搜索方向是相互共轭的。
搜索方向? $d_k$ 仅仅是? $-g_k$ 和? $d_{k-1}$ 的线性组合。

不妨建立? $d_k$ 和 $d_{k-1}$ ?的关系如下：

$d_k=-g_k+\\beta_{k-1}d_{k-1}\\\\$

那么 $\\beta_{k-1}$ ?怎么确定呢？我们可以使用共轭的性质，在等式的两边同乘 $d_{k-1}^TQ$ ?，并利用 $d_{k-1}^TQd_k=0$ ?：

$\\beta_{k-1}^{HS}=\\frac{g_k^TGd_{k-1}}{d_{k-1}^TGd_{k-1}}\\\\$

上述公式称为Hestenes-Stiefel公式，由于我们使用了共轭的性质来确定我们的系数 $\\beta$ ?，加上子空间拓展定理，我们能保证我们得到的方向与之前的搜索方向是共轭的。

由于Hestenes-Stiefel公式中有矩阵，我们还可以优化公式，让其中的矩阵消失，这样做有两个好处：

这样可以使得共轭梯度法也能适用于非二次型函数（当然只是形式上，具体的收敛性还需要论证，此处省略）
对于计算机来说，把矩阵运算变成向量运算可以降低空间复杂度和时间复杂度。

由于 $g_{k+1}-g_k=G(x_{k+1}-x_k)=\\alpha Gd_k$ ?，所以Hestenes-Stiefel公式可以修改为Crowder-Wolfe公式：

$\\beta_{k-1}^{CW}=\\frac{g_k^T(g_k-g_{k-1})}{d_{k-1}^T(g_k-g_{k-1})}\\\\$

我们还可以进一步优化，使得我们的式子中只出现梯度信息，我们在式子 $d_k=-g_k+\\beta_{k-1}d_{k-1}$ ?两边取转置并右乘上 $g_{k+1}$ ?得到 $d_k^Tg_{k+1}=-g_k^Tg_{k+1}^T+\\beta_{k-1}d_{k-1}^Tg_{k+1}$ ?，根据子空间拓展定理，我们有 $d_k^Tg_{k+1}=d_{k-1}^Tg_{k+1}=0$ ?，所以我们有 $g_{k+1}^Tg_k=0$ ?。这说明在共轭梯度法中，相邻的两次搜索得到的梯度相互正交。

注意到? $d_{k-1}^Tg_{k-1}=(-g_{k-1}+\\beta_{k-2}d_{k-2})^Tg_{k-1}=-g_{k-1}^Tg_{k-1}$ 。代入Crowder-Wolfe公式可得：

$\\beta_{k-1}=\\frac{g_k^T(g_k-g_{k-1})}{d_{k-1}^T(g_k-g_{k-1})}=\\frac{g_k^Tg_k}{-d_{k-1}^Tg_{k-1}}=\\frac{g_k^Tg_k}{g_{k-1}^Tg_{k-1}}\\\\$

所以Crowder-Wolfe公式可以修正为Fletcher-Reeves公式：

$\\begin{align}\\beta_{k-1}^{FR}=\\frac{g_k^Tg_k}{g_{k-1}^Tg_{k-1}}\\end{align}\\\\$

过程中我们还得到了 $\\beta_{k-1}=-\\frac{g_k^Tg_k}{d_{k-1}^Tg_{k-1}}$ ?。这个修正式我们称为Dixon公式。等价的共轭梯度公式很多，此处只列出了几个。我们可以总结一下：

$\\begin{align}\\beta_{k-1}^{HS}&=\\frac{g_k^TGd_{k-1}}{d_{k-1}^TGd_{k-1}}\\quad\\quad\\quad(\\bold{Hestenes-Stiefel公式})\\\\ \\beta_{k-1}^{CW}&=\\frac{g_k^T(g_k-g_{k-1})}{d_{k-1}^T(g_k-g_{k-1})}\\quad\\quad(\\bold{Crowder-Wolfe公式})\\\\ \\beta_{k-1}^{FR}&=\\frac{g_k^Tg_k}{g_{k-1}^Tg_{k-1}}\\quad\\quad\\quad\\quad\\quad(\\bold{Fletcher-Reeves公式})\\\\ \\beta_{k-1}^D&=-\\frac{g_k^Tg_k}{d_{k-1}^Tg_{k-1}}\\quad\\quad\\quad\\quad(\\bold{Dixon公式})\\\\ \\beta_{k-1}^{PRP}&=\\frac{g_k^T(g_k-g_{k-1})}{g_{k-1}^Tg_{k-1}}\\quad\\quad\\quad(\\bold{Polak-Ribiere-Polyak公式})\\\\ \\beta_{k-1}^{DY}&=\\frac{g_k^Tg_k}{d_{k-1}^T(g_k-g_{k-1})}\\quad\\quad(\\bold{Dai-Yuan公式})\\\\ \\end{align}\\\\$

以上公式在函数为二次型，且使用精准线搜时完全等价。实际使用中，我们常使用FR和PRP，因为这两个公式只需要梯度信息。

注意到，上述公式只是给定了共轭方向的迭代公式，但是对于第一个搜索方向，我们无法通过上述公式获取。为了满足共轭方向法中的 $d_k^Tg_k<0$ ?也就是我们选取的共轭方向至少是个下降方向，我们一般就直接把共梯度法的第一步当作梯度下降法，也就是选取梯度的反方向作为我们的第一个搜索方向。

应用以上的结论，我们也可以轻易地计算步长 $\\alpha_k$ ?的值。注意到 $g_{k+1}-g_k=G(x_{k+1}-x_k)=\\alpha_kGd_k$ ?。两边左乘? $d_{k}^T$ 得到：

$\\alpha_k=\\frac{d_k^T(g_{k+1}-g_k)}{d_k^TGd_k}=-\\frac{d_k^Tg_k}{d_k^TGd_k}=\\frac{g_k^Tg_k}{d_k^TGd_k}\\\\$

结合上述共轭方向的迭代式， $\\beta$ ?的求法，还有步长公式，我们大致已经可以整理出一个完整的共轭梯度法了。使用FR公式的共轭梯度法的框架如下：（假定我们优化的函数时二次型）
$\\begin{align}首先给出&迭代初值x_0，阈值\\epsilon>0\\\\ 计算梯度&值g_0=Gx_0+b,令d_0=-g_0,k=0,重复以下步骤：\\\\ &1.\\quad如果||g_k||<\\epsilon,停止迭代。\\\\ &2.\\quad计算步长：\\alpha_k=\\frac{g_k^Tg_k}{d_k^TGd_k}\\\\ &3.\\quad更新迭代点：x_{k+1}=x_k+\\alpha_kd_k\\\\ &4.\\quad计算新的梯度：g_{k+1}=Gx_{k+1}+b\\\\ &5.\\quad计算组合系数：\\beta_k=\\frac{g_{k+1}^Tg_{k+1}}{g_k^Tg_k}\\\\ &6.\\quad计算共轭方向：d_{k+1}=-g_{k+1}+\\beta_kd_k\\\\ &7.\\quad令k=k+1,转第2步。 \\end{align}\\\\$

我们可以用一道题来练练手：用FR共轭梯度法求解下属无约束优化问题，并给出共轭向量组。

$\\min f(x)=\\frac32 x_1^2+\\frac12x_2^2-x_1x_2-2x_1\\\\$

解：

首先化成向量形式： $f(x)=\\frac12x^TGx+b^Tx,G=\\begin{pmatrix}3&-1\\\\-1&1\\end{pmatrix},b=(-2,0)^T,g(x)=Gx+b$ ?.

很明显，这个问题是有一个最优点的，所以我们就不设阈值了，一直算到梯度为0为止。

设 $x_0=(0,0)^T$ ?，易知? $g_0=Gx_0+b=(-2,0)^T\\quad d_0=-g_0=(2,0)^T\\quad$ 。接下来试试FR共轭梯度法：

$\\begin{align}\\alpha_0&=\\frac{g_0^Tg_0}{d_0^TGd_0}=\\frac{1}{3}\\\\ x_1&=x_0+\\alpha_0 d_0=(\\frac23,0)^T\\\\ g_1&=Gx_1+b=(0,-\\frac23)^T\\\\ \\beta_0&=\\frac{g_1^Tg_1}{g_0^Tg_0}=\\frac19\\\\ d_1&=-g_1+\\beta_0d_0=(\\frac29,\\frac23)^T\\\\\\\\ \\alpha_1&=\\frac{g_1^Tg_1}{d_1^TGd_1}=\\frac32\\\\ x_2&=x_1+\\alpha_1d_1=(1,1)^T\\\\ g_2&=Gx_2+b=(0,0)^T \\end{align}\\\\$

因此，最终得到的最优点为? $x_2=(1,1)^T$ 。获取的共轭向量组为? $d_0=(2,0)^T,d_1=(\\frac29,\\frac23)^T$ 。

关于共轭梯度法的几个好用的性质，其实我们已经在推导FR的过程中得到了：

共轭性： $d_i^TGd_j=0,j\ ot=i$ ?。
正交性： $g_i^Tg_j=0,j\ ot=i$ ?。
下降性：? $d_i^Tg_i=-g_i^Tg_i$ 。

除了共轭性外，其他的两条性质都可以通过 $d_k=-g_k+\\beta_{k-1}d_{k-1}$ ?得到

限于篇幅（笔者太懒），共轭梯度法的收敛速率只给出结论，不做证明。

设目标函数的条件数为? $\\kappa(G)=||G||_2||G^{-1}||_2$ ，则共轭梯度法产生的点列误差估计为：

$\\frac{||x_{k+1}-x^*||_G}{||x_k-x^*||_G}\\le\\frac{\\sqrt{\\kappa(G)}-1}{\\sqrt{\\kappa(G)}+1}\\\\$

所以可以看出来，共轭梯度法是线性收敛的，而且与梯度下降法相比有更快的收敛速率（与梯度下降法比起来，共轭梯度的收敛速率就是把 $\\kappa$ 替换成了 $\\sqrt{\\kappa}$ ）。通过改善 $G$ 的条件数，可以加快收敛速度。

我们之前的算法和分析都是建立在研究的函数是二次型的假设下，这未免过于理想，要知道，深度学习中大部分loss关于前馈网络参数的函数甚至都不是凸函数，那么将我们得到的共轭梯度法进行泛化就显得很有必要了。而Fletcher和Reeves在1964提出了针对菲尔茨函数的共轭梯度法FR-CG：

$\\begin{align}首先给出&迭代初值x_0，阈值\\epsilon>0\\\\ 计算梯度&值g_0=Gx_0+b,令d_0=-g_0,k=0,重复以下步骤：\\\\ &1.\\quad如果||g_k||<\\epsilon，停止迭代\\\\ &2.\\quad通过线搜索算法获取步长\\alpha_k\\\\ &3.\\quad更新迭代点：x_{k+1}=x_k+\\alpha_kd_k\\\\ &4.\\quad计算新的梯度：g_{k+1}=\ abla f(x_{k+1})\\\\ &5.\\quad计算组合系数：\\beta_k=\\frac{g_{k+1}^Tg_{k+1}}{g_k^Tg_k}\\\\ &6.\\quad计算共轭方向：d_{k+1}=-g_{k+1}+\\beta_kd_k\\\\ &7.\\quad令k=k+1,转第2步。 \\end{align}\\\\$

你会发现，这个算法其实和之前的没有区别，我们的 $\\beta_{k}$ ?的计算方法是依照二次型的前提得出的，除了? $\\beta_k$ 的计算，其他变量的得出和优化函数的具体表达式没有关系。所以我们需要提出疑惑，这玩意儿放在非二次型问题上能够收敛吗？

事实上，FR共轭梯度法收敛性已经被证明，由于笔者很懒，所以直接给出吧。。。

$\\begin{align}&设f:\\mathbb R^n\ o\\mathbb R在有界水平集L=\\{x\\in\\mathbb R^n|f(x)\\le f(x_0)\\}上连续可微并且有\\\\ &下界，则采用精确线搜索的FR共轭梯度法产生的序列x_k至少有一个聚点是驻点，即：\\\\\\\\ &1.\\quad如果\\{x_k\\}是有限序列，其最后一个点是f(x)的驻点。\\\\ &2.\\quad如果\\{x_k\\}是无限序列，其必有一个聚点，并且任意聚点都是f(x)的驻点。 \\end{align}\\\\$

在讨论FR共轭梯度法前，我觉得有必要先复习一下，梯度下降法，牛顿法，拟牛顿法下降的条件：

梯度下降法：一定下降。
牛顿法：若迭代点处的Hessian矩阵正定，则一定下降。
拟牛顿法：以DFP为例，若 $s_k^Ty_k>0$ ?，则该步一定下降。

关于FR-CG的下降性，我们需要分类讨论。

如果我们采用精准线搜，则根据共轭梯度的性质，我们有 $g_k^Td_k=-g_k^Tg_k=-||g_k||^2$ ?。若 $||g_k||=0$ ?，则已经达到最优点；若 $||g_k||\ ot=0$ ?，则 $g_k^Td_k=-||g_k||^2<0$ ?。一定是下降方向。
若我们采用强Wolfe准则进行非精确线搜索，则一定有 $g_k^Td_k<0$ ?。一定是下降方向。
对于其他的非精确线搜索，不能保证其下降性。