在众多优化算法在中，Adam是我使用体验感最好的优化算法。相比诸多飘渺的智能算法如遗传或PSO之类，Adam在我看来才更像数学，具有严谨的理论推导以及可操作性，对参数约束起来也更加容易，质朴但实用。

初次接触到 Adam 优化算法时，只知道Adam有着自适应的学习率已经更快的收敛速度，但在接触了数字信号处理之后，才幡然醒悟：

Adam 优化算法事实上就是实现了IIR数字滤波器，对梯度信号进行滤波

文章中所有代码文件都上传至GitHub:

https://github.com/Z-MiCTrue/Adam-plushttps://github.com/Z-MiCTrue/Adam-plus

1.整体流程

2. 核心：IIR数字滤波器对梯度信号进行滤波

如果说Momentum-SGD是将物理中的动量概念加入到了梯度下降里，我则更愿意相信Adam是将数字信号处理中IIR滤波器的概念考虑了进来：

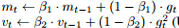
这两行便是Adam的核心，假如令，将其一展开便可得到：

若把每一次迭代后计算得到的梯度看作是一个冲激信号，那么随着迭代次数的增加，该冲激信号乘以其所对应的权重后，在时间上将呈现为如下一个指数衰减信号：

即，该式等效于：将冲激序列（历史梯度）与指数衰减序列卷积；

换一种说法，假设这是一个线性时不变系统，则??、?对单位脉冲信号的响应（系统函数）为指数衰减函数。

同时，单个为指数衰减函数的系统函数，其表达形式为：

?

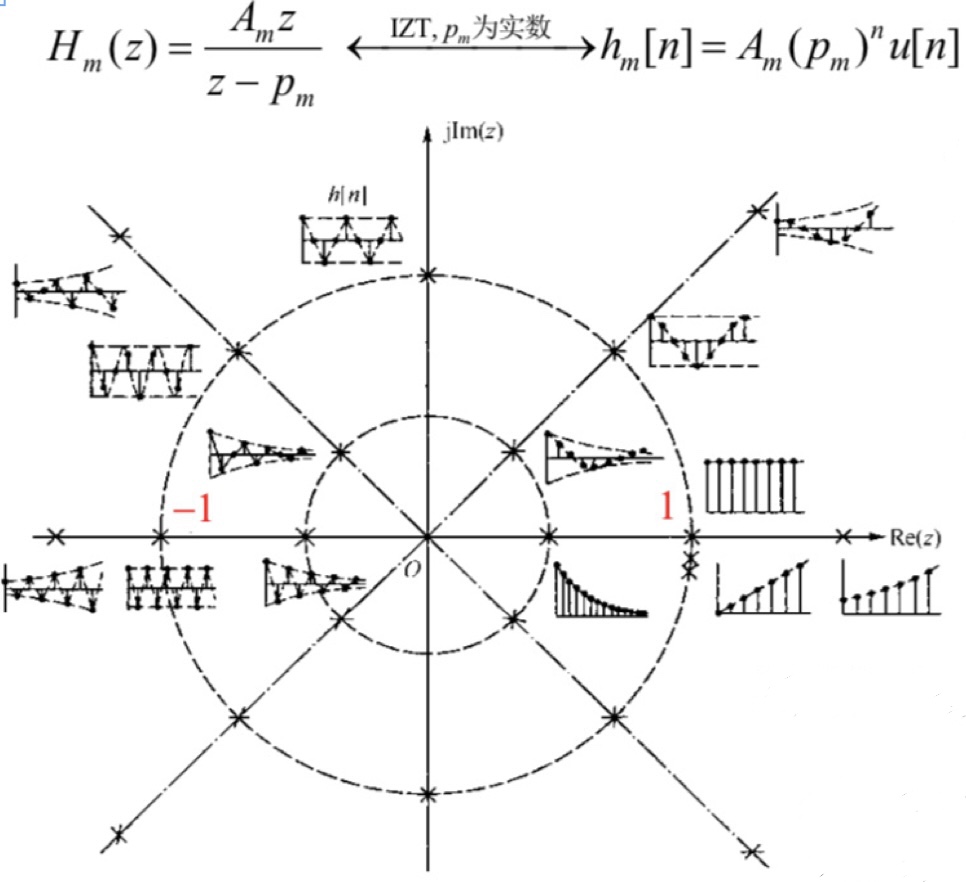而IIR数字滤波器的系统函数表示形式为：

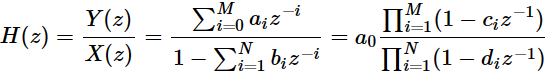
即Adam中对历史梯度的处理，可以看成一个 a_1... = 0; b_0,2... = 0 的IIR数字滤波处理，??是对梯度的滤波；??是对梯度平方的滤波（反应幅值）。而后面对误差的修正，在我看来，主要是为了修正零状态响应所带来的影响。

所以，从这个角度看，如果想增加Adam对梯度的敏感性，有两种途径：

1.增加迭代时的项数，即使其变为高阶滤波器

2.增大??值；

反之亦然

3. 整体来看Adam

在不加偏移修正项的情况下，由上一部分可得出 Adam 的等效公式为：

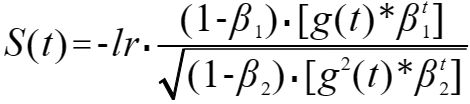
?其中 S(t) 为最终的步长序列；

? ? ? ? ?g(t) 为梯度序列；

为验证该式的正确性以及研究单位冲激信号为整个系统带来的单位冲激响应（系统函数），我使用了以下代码：

使用迭代计算出的结果：

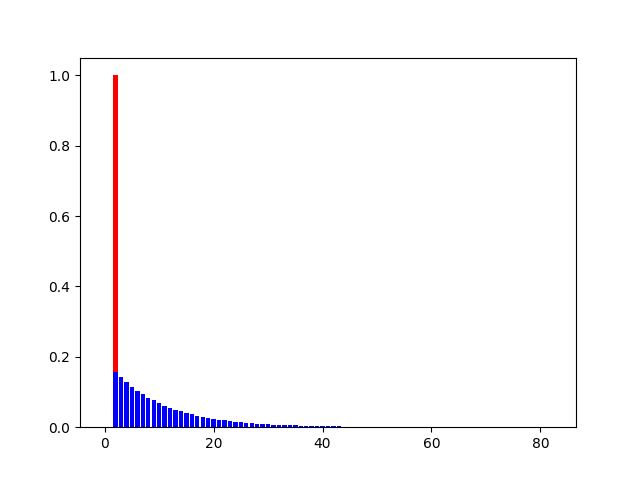
使用等效计算式计算出的结果（因为是完全卷积，所以结果序列长度为输入长度的两倍）：

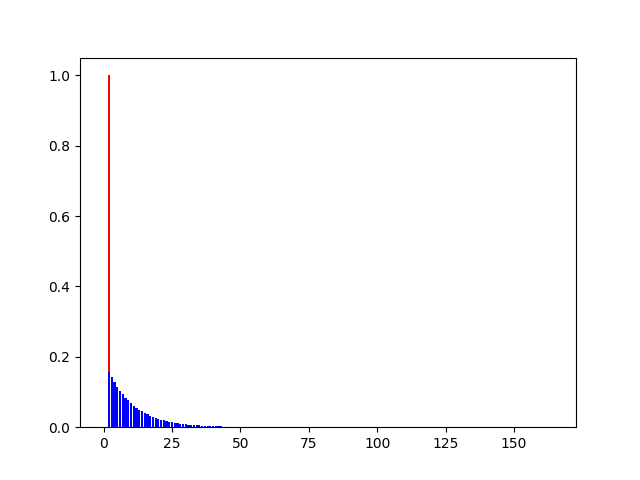
添加入偏移修正项的结果 ：

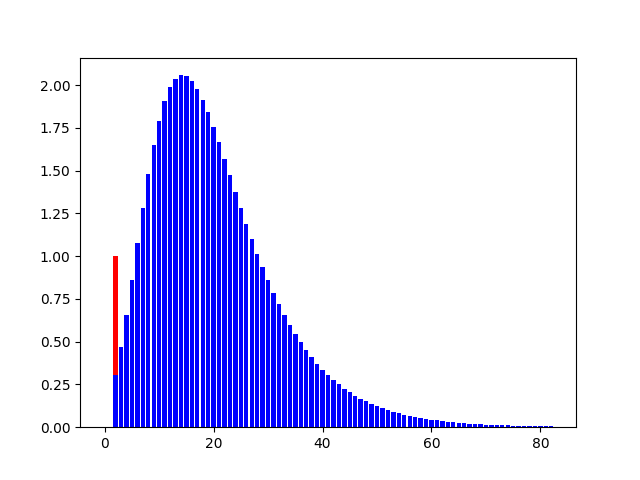
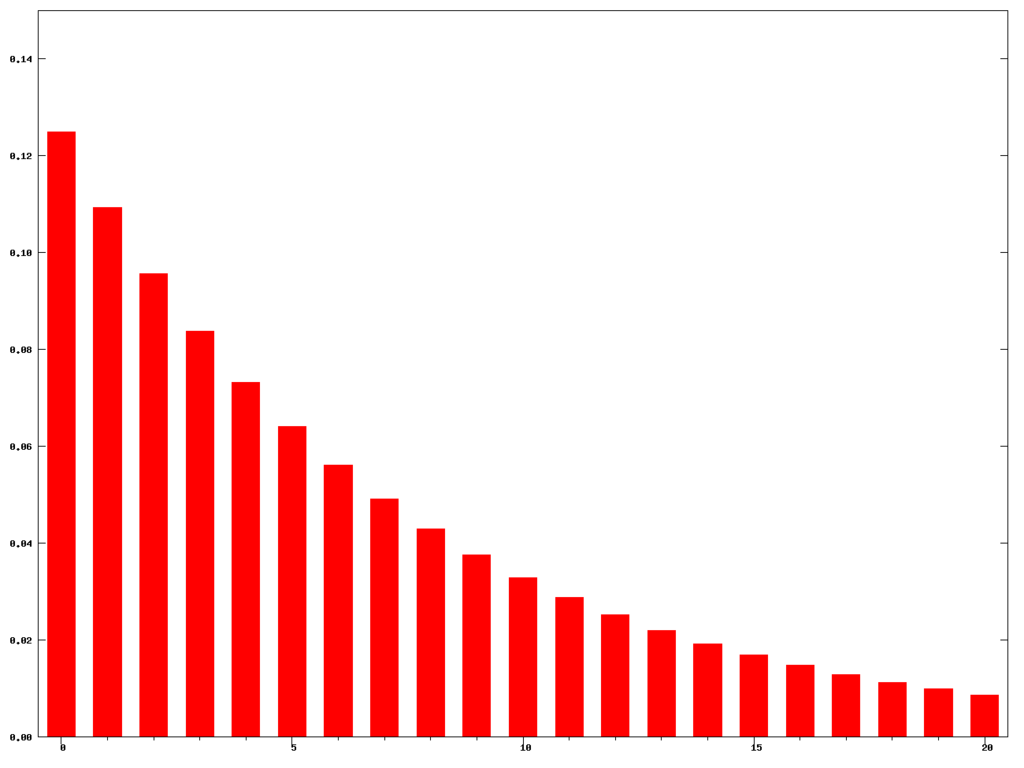
# 其中：红色为单位冲激序列，蓝色为单位冲击响应序列?

? ? ? ? ? ? ? 以上数据所采用的参数为：

于是可以得到以下结论：

? ? ? 等效计算式具有正确性；

? ? ? ? 偏移修正项对整体系统的单位冲激响应影响显著，具体表现为：

? ? ? ? ? ? ? ? 从幅值上看，添加偏移修正项相比未添加对梯度的敏感性有显著提高，添加后最大为2倍，而未添加则仅为0.18倍左右；

从响应时间上看，添加偏移修正项相比未添加在响应时间上有着约15次迭代的延迟，而这就正意味着：冲激响应在冲激到来后并不会立刻达到峰值，换一种说法就是仍具有一定动量，提高了在局部最小值点的逃逸能力。

# 由于添入偏移修正项后，等效计算式过于复杂（包含了累乘以及二次卷积）所以这里并没有给出

综上，可以得出以下结论：

1.增加迭代时的项数，即使其变为高阶滤波器 或增大??值， 可增加Adam对梯度的敏感性；

2.偏移修正项在增加了Adam对梯度敏感性的同时，也为其增加了在局部最小值点的逃逸能力；

3.lr ( 学习率 ) 对优化效果的影响至关重要，其限制了实际每次迭代步长的上限。所以设置过小将导致算法在甚至数万次的迭代后仍无法收敛，设置过大则会导致其对梯度过于敏感同样影响收敛。使用时需根据具体场景做出合适选择。

整体代码

该代码在实现Adam的基础上，我做了如下改动:

1.以小量近似计算导数，虽然牺牲了一部分精确度，但拓展了其应用范围（如损失函数中存在逻辑判断，或者有整数限制），避免了复杂的求导过程

2.增加了参数范围限制，以应对一些带有边界限制的优化问题

3.计算矩阵化，可同时从多个起点开始批量梯度下降，提高运行效率

4.增加了对学习率 lr 的检查过程，以在学习率设置过小时提出警告

5.增加了保留历史最佳项的过程。因为滤波的存在，所以迭代结束时的结果可能并不是历史最优结果

实例化优化器

其中 integrate 正是 近似求导时的小量步长，如果参数要求为整数（如：优化每次生产商品的个数），则可以设置为1。如需各向异性，则可修改为一数组（如：Oa.integrate=np.array([0.1, 1]))

设置初始值

这里设置的初始种子数目和优化参数数目，需与实例化优化器时的设置的一致，优化器将同时批量对其进行迭代。该项是可选项，如果不加说明，优化器将默认从在参数约束范围里随机生成对应数量的种子。

设置参数约束范围

该项为可选设置，如果不加说明，优化器将默认优化范围为整个实数域

指定目标函数

这里将函数入口地址赋给优化器，以供后面调用

开始优化

*检查lr状态

该段代码的作用是在迭代次数达到上限时检查lr是否设置的过小，导致优化空间仍然巨大。通过在迭代中设置多个检查点，判断迭代结束时，当前检查点的优化程度是否相比上一个检查点有显著降低。如果没有，则说明仍有很大的优化空间，学习率lr设置过小。

期待提供改进建议，感谢 Totutod 提供了信号方面的指导，Thanks！

参考文献：

[1] Kingma D , ?Ba J . Adam: A Method for Stochastic Optimization[J]. Computer Science, 2014.